Derivadas, intersecciones y asíntotas de croquis de curvas

Croquizado de curvas – Introducción

Al comenzar el cálculo, se hace hincapié en derivar las propiedades de las funciones. Las propiedades de la función se pueden agrupar en las siguientes categorías:

(1) dominio, rango y simetría,

(2) límites, continuidad y asíntotas,

(3) derivadas y tangentes, y

(4) valores extremos, intervalos de aumento y disminución, concavidad y puntos de inflexión.

En esta lección, la información enumerada en las cuatro categorías generales se aprovecha para esbozar los gráficos de funciones que revelan las características importantes de las funciones. La siguiente lista de verificación pretende ser una guía para dibujar una curva y = f (x) a mano. Al aplicar la lista de verificación para bosquejar una función, no todos los elementos son relevantes para todas las funciones. Por ejemplo, es posible que una gráfica no tenga una asíntota o no posea intersecciones con el eje x.

Intercepta

La intersección con el eje y de la función es f (0) y esto indica dónde la curva se cruza con el eje y.

Para encontrar las intersecciones con x, establezca y = 0 y resuelva para x. Esto puede implicar tener que usar división sintética para polinomios de alto orden, identidades trigonométricas para funciones trigonométricas o reglas logarítmicas para funciones exponenciales. Este paso puede omitirse si la ecuación es computacionalmente difícil de resolver.

Asíntotas

Desde el cálculo, si se cumple el siguiente cálculo de límite:

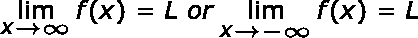entonces la línea y = L es una asíntota horizontal de la curva y = f (x). Si

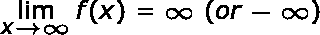Las asíntotas horizontales de funciones racionales se pueden encontrar observando los exponentes de los términos de mayor grado en el numerador y denominador.

• Si el término con el exponente más alto en el numerador tiene el mismo exponente que el término con el exponente más alto en el denominador, entonces hay una asíntota horizontal en y es igual a la razón de sus coeficientes.
• Si el exponente del término principal en el denominador es menor que el exponente del término principal del numerador, entonces no hay asíntota horizontal.
• Si el exponente del término principal del denominador es mayor que el exponente del término principal del numerador, entonces hay una asíntota en y es igual a cero.

La línea x = a es una asíntota vertical si al menos una de las siguientes afirmaciones es verdadera:

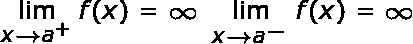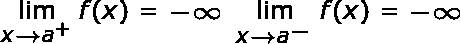Para funciones racionales, las asíntotas verticales pueden ubicarse equiparando el denominador a cero después de cancelar cualquier factor común.

Además, las funciones racionales pueden tener asíntotas inclinadas si el grado del numerador es uno más que el grado del denominador. La asíntota inclinada es el cociente resultante de una división larga.

Usar derivados

Los números críticos de una función son los números c donde f ‘(c) = 0 o f’ (c) no existe. Si f ‘cambia de positivo a negativo en un número crítico c , entonces f (c) es un máximo local. Si f ‘cambia de negativo a positivo en c , entonces f (c) es un mínimo local. Este procedimiento se conoce como prueba de la primera derivada.

Alternativamente, si f ‘(c) = 0 y f’ ‘(c) no es cero, entonces f’ ‘(c)> 0 implica que f (c) es un mínimo local y f’ ‘(c) <0 implica que f (c) es un máximo local. Este procedimiento se conoce como prueba de la segunda derivada. Además, la curva es cóncava hacia arriba donde f ” (x)> 0 y cóncava hacia abajo donde f ” (x) <0. Los puntos de inflexión ocurren donde cambia la dirección de la concavidad .

Ejemplo

Utilice los métodos de esta lección para dibujar la curva:

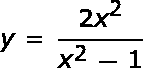(1) El dominio es:

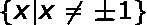(2) Las intersecciones en x y en y son ambas 0.

(3) Las asíntotas se calculan de la siguiente manera:

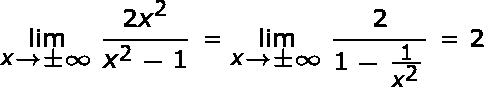Por tanto, la recta y = 2 es una asíntota horizontal.

Dado que el denominador es 0 cuando x = 1 ox = -1, entonces, según los siguientes cálculos de límite,

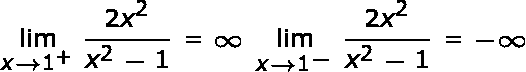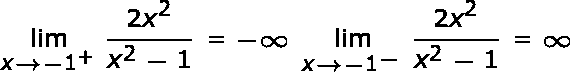Por tanto, las rectas x = 1 y x = -1 son asíntotas verticales.

(4) Utilizando la regla del cociente para la diferenciación, la primera derivada se calcula como

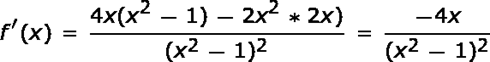El único número crítico es x = 0. Dado que f ‘cambia de positivo a negativo en 0, f (0) = 0 es un máximo local según la prueba de la primera derivada.

La segunda derivada es

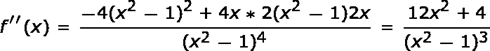Dado que el numerador es siempre mayor que cero, f ” (x)> 0 si y solo si | x | > 1 y f ” (x) <0 si y solo si | x | <1. Por tanto, la curva es cóncava hacia abajo en el intervalo abierto (-1, 1) y es cóncava hacia arriba en todos los demás lugares. No hay punto de inflexión ya que -1 y 1 no están en el dominio de f.

Combinando todos los cálculos anteriores, el esquema de la curva es como se muestra:

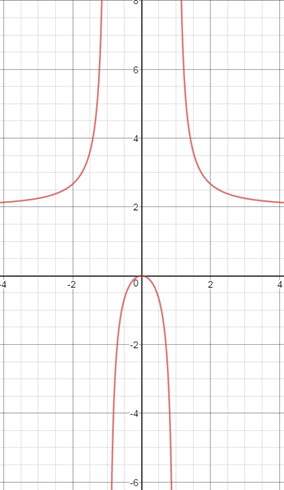Resumen de la lección

Los pasos del bosquejo de curvas presentados en esta lección son solo algunos de los esenciales necesarios para graficar una función. Las asíntotas horizontales y verticales se pueden calcular tomando los límites apropiados de una función. Las intersecciones en y de una función se encuentran estableciendo x igual a cero. Las intersecciones con el eje x de una función se encuentran estableciendo la función igual a cero y resolviendo las raíces. Los números críticos identifican puntos en el gráfico que son máximos relativos o mínimos relativos. La segunda derivada de una función indica en qué intervalos la función es cóncava hacia arriba o cóncava hacia abajo.