Encontrar la serie de Maclaurin para Sin (x)
Calculadoras y funciones trigonométricas
Antes de que las calculadoras científicas se generalizaran, los libros de texto de matemáticas solían contener tablas trigonométricas. Estas tablas se utilizaron para encontrar valores para varias funciones trigonométricas como el seno. Para encontrar el seno de cierto ángulo, los estudiantes tendrían que buscarlo en una tabla. Si un estudiante no tuviera un libro de texto o una mesa, no podría determinar el seno de un ángulo.
Sin embargo, hoy podemos usar calculadoras, que a menudo se encuentran incluso en nuestros teléfonos inteligentes, para simplemente conectar y tomar valores para la función sinusoidal. ¿Cómo lo hacen nuestras calculadoras con tanta facilidad? Las calculadoras suelen utilizar la serie de Maclaurin para seno para determinar de forma rápida y precisa los valores de la función seno.
¿Qué es una serie Maclaurin?
Una serie de Maclaurin es una forma en que podemos representar ciertas funciones, incluida la función seno, usando una suma infinita de potencias enteras de x. En general, una serie de Maclaurin para una función f ( x ) se ve así:
 |
Recuerde, el símbolo Σ nos dice que estamos sumando términos de acuerdo con la fórmula a la derecha del símbolo. La ecuación inferior nos dice el primer número que ingresamos para n , mientras que el número superior nos dice el último número que ingresamos para n . Como tenemos ∞ en la parte superior, esta es una serie infinita o una en la que sumamos un número infinito de términos.
Analicemos la fórmula a la derecha de Σ. Recuerda que n ! significa que multiplicamos todos los números naturales del 1 al n juntos. Entonces, por ejemplo, ¡5! = 1 × 2 × 3 × 4 × 5. Luego, ƒ ( n ) (0) representa la n- ésima derivada de ƒ evaluada en 0.
Cálculo de la serie de Maclaurin para Sin ( x )
En este punto, puede estar pensando que no hay más trabajo por hacer para encontrar la serie de Maclaurin para sin ( x ). Sin embargo, para que la serie sea más útil, veremos si podemos encontrar un patrón en las derivadas de la función seno. En otras palabras, para ayudar a la calculadora a usar la serie de Maclaurin, veremos si podemos escribir la serie de Maclaurin para la función seno sin usar la notación ƒ ( n ) (0). La siguiente tabla muestra hasta la quinta derivada del seno. Vea si puede encontrar un patrón.
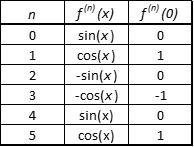 |
Cual es el patron? Resulta que ƒ ( n ) (0) = ± 1 cuando n es impar y 0 cuando n es par. Por lo tanto, escribir la serie de Maclaurin para sin (x) nos da lo siguiente.
 |
Simplificar esto produce lo siguiente.
 |
Para escribir esto con la notación Σ, tendremos que encontrar un patrón para los términos distintos al que se usó para hacerlo, ya que todas las demás potencias de x han desaparecido. Observa que solo tenemos potencias impares de x y los números impares correspondientes en la parte inferior de cada fracción. Dado que los números impares comienzan en 1 y aumentan en 2 con cada término, podemos representarlos en la suma con la expresión 2 n + 1, donde n es el número del término. A continuación, necesitamos representar que los términos alternan entre positivo y negativo. Podemos hacer esto usando (-1) n , ya que multiplicar -1 por sí mismo alternativamente produce 1 y -1.
Por tanto, podemos escribir lo siguiente.
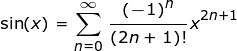 |
¿Cómo usa una calculadora la serie Maclaurin?
Quizás se esté preguntando: “Si una serie de Maclaurin es una serie infinita, ¿cómo la usa mi calculadora?” ¿No tomaría una cantidad infinita de tiempo usarlo? ”. Se necesitaría una cantidad infinita de tiempo para intentar calcular completamente el valor de una serie de Maclaurin en un punto particular. Es por eso que su calculadora no usa la serie completa. Solo usa una parte. La cantidad de términos que se usan puede variar de una calculadora a otra, pero dado que las calculadoras pueden sumar, restar, multiplicar y dividir muy rápidamente, usar una gran cantidad de términos en la serie, incluso hasta 100, es muy factible para una calculadora. Por lo tanto, el valor que le da su calculadora para el seno de un número es en realidad una aproximación. Sin embargo, debido a la naturaleza de la serie Maclaurin, es una aproximación muy, muy precisa.
Resumen de la lección
Para evitar tener que almacenar tablas trigonométricas, las calculadoras utilizan una serie de Maclaurin para calcular el valor de sin ( x ). Una serie de Maclaurin para una función es una serie dada por lo siguiente.
 |
Usando esta definición de una serie de Maclaurin, podemos determinar que la función seno se puede representar de la siguiente manera.
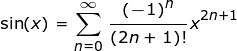 |
Articulos relacionados
- Imagenología Médica: rayos X, resonancia magnética
- Teoría X y Teoría Y de McGregor: Definición y tipos de gerentes
- Entre lo Oculto: Autor, Serie y Género
- Los juegos del hambre: autor y serie
- Encontrar constantes de velocidad y ordenar reacciones: gráfico y ley de velocidad
- Lección de plantas con flores y sin flores
- Malcolm X: Biografía, asesinato e impacto
- Malcolm X y el nacionalismo negro en el movimiento por los derechos civiles
- La autobiografía de Malcolm X por Alex Haley: resumen y análisis
- Hipoglucemia sin diabetes: síntomas y tratamiento
