Inercia rotacional: Laboratorio de física

¿Qué es la inercia rotacional?

La inercia rotacional , también conocida como momento de inercia , es el equivalente rotacional de la masa; una cantidad que resiste cambios en la rotación de un objeto. El movimiento de rotación es similar al movimiento lineal. En el movimiento lineal, los objetos más masivos resisten cambios en su velocidad; en movimiento rotacional, los objetos con más inercia rotacional resisten cambios en su velocidad angular. Un objeto con más masa tendrá más inercia rotacional, pero la forma en que la masa se distribuye alrededor del punto de rotación también tiene un efecto sobre la inercia rotacional. Si su masa está muy lejos del punto de rotación, el objeto tiene más inercia rotacional que si estuviera cerca.

Hoy vamos a investigar la inercia rotacional e intentaremos calcular un valor de inercia rotacional para un volante.

Pasos del laboratorio de física

Para este laboratorio de física, necesitará:

• Un volante
• Un eje para el volante
• Un soporte para el eje que le permitirá girar
• Una percha de peso
• Pesos ranurados
• Un cronómetro
• Una regla de metro
• Cuerda
• Cinta adhesiva
• Un transportador

Paso 1: Ensamble el equipo. El volante debe estar en el eje y el eje debe estar unido a su soporte, lo que le permite girar libremente. Coloque un trozo de cinta adhesiva en el costado del volante para que pueda ver con mayor precisión cómo gira.

Paso 2: Ate un extremo de una cuerda larga a un soporte fijo cerca del eje, luego enrolle la cuerda alrededor del eje hasta que quede poca cuerda libre.

Paso 3: coloque algunas pesas en la percha y ate el otro extremo de la cuerda a la parte superior de la percha. El peso debe colgar no muy por debajo del eje.

Paso 4: Mida la altura de la masa colgante sobre el suelo.

Paso 5: suelta la masa y déjala caer por gravedad. Inicie el cronómetro al mismo tiempo y mida el tiempo que tarda en llegar al suelo. Repita cinco veces y anote sus números.

Paso 6: Calcula el promedio de tus intentos sumando los números y dividiendo por cinco.

Paso 7: haz otras cinco pruebas, pero esta vez concéntrate en el volante. Usa el trozo de cinta para medir cuántas veces gira la rueda durante el movimiento. Para que su número sea lo más preciso posible, use el transportador para medir las posiciones inicial y final. Por ejemplo, quizás su rueda giró 6.25 veces, porque giró 6 círculos completos y luego terminó 90 grados más allá de su posición inicial.

Paso 8: Calcula el promedio de tus intentos sumando los números y dividiéndolos por cinco.

Paso 9: Usa la regla para medir el radio del volante.

Puede registrar sus datos en una tabla que se parece a esto:

Tabla de datos de ejemplo

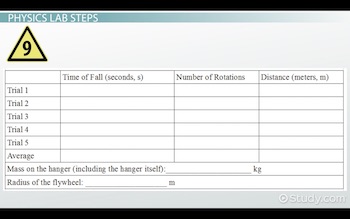Si aún no lo ha hecho, ahora es el momento de pausar el video y comenzar. ¡Buena suerte!

Análisis de los datos

Ahora que tiene sus datos, es hora de analizarlos. En este movimiento, la energía potencial gravitacional de la masa se convierte en energía cinética. Pero debido a que la masa también hace girar el volante, parte de la energía potencial gravitacional se convierte en energía de rotación. Por lo tanto, podemos decir que la energía potencial gravitacional en la masa al inicio es igual a la energía cinética en la masa justo antes de que toque el suelo más la energía de rotación en el volante justo antes de que toque el suelo.

Entonces mgh es igual a 1/2 mv al cuadrado más ½ I omega al cuadrado. Aquí, m es la masa colgante en kilogramos, g es la aceleración debida a la gravedad (que es 9,8 en la Tierra), h es la altura a la que cae la masa en metros, v es la velocidad de la masa antes de que golpee el suelo en metros por segundo, I es la inercia rotacional del volante en kilogramos metros cuadrados, que estamos tratando de encontrar, y omega es la velocidad angular del volante en radianes por segundo.

En primer lugar, puede calcular v tomando la distancia al suelo y dividiéndola por el tiempo promedio que tardó en llegar al suelo y luego multiplicándolo por dos. La razón por la que tienes que multiplicarlo por dos es porque la velocidad de la masa cuando llegue al piso será aproximadamente el doble de la velocidad promedio de la masa durante la caída.

M es igual a la masa en la percha que midió, g es 9.8, h es la distancia al suelo, I es lo que estamos tratando de encontrar y omega se puede calcular a partir de esta ecuación:

Ecuación para calcular omega

Omega es igual a 2 veces pi, multiplicado por el radio del volante multiplicado por el número medio de rotaciones que midió dividido por el tiempo medio que tardó la masa en llegar al suelo. Inserte todos estos números en la ecuación y resuelva para encontrar el momento de inercia del volante.

Y eso es; ya terminaste.

Resumen de la lección

La inercia rotacional , también conocida como momento de inercia , es el equivalente rotacional de la masa; una cantidad que resiste cambios en la rotación de un objeto. Al igual que con el movimiento lineal, los objetos más masivos resisten los cambios en su velocidad. En el movimiento de rotación, los objetos con más inercia de rotación resisten los cambios en su velocidad angular. Un objeto con más masa tendrá más inercia rotacional, pero la forma en que la masa se distribuye alrededor del punto de rotación también tiene un efecto sobre la inercia rotacional. Si su masa está muy lejos del punto de rotación, el objeto tiene más inercia rotacional que si estuviera cerca.

Usando estos conceptos y una ecuación de energía, pudimos investigar la inercia rotacional, calculándola para un volante.

Los resultados del aprendizaje

Una vez que haya terminado con esta lección, podrá:

• Definir inercia rotacional
• Describe los factores que afectan la inercia rotacional.
• Crea una ecuación y un experimento para explicar la inercia rotacional.