Objetos que se mueven en círculos verticales: análisis y problemas de práctica

Movimiento en un círculo vertical

En otra lección, hablamos sobre el movimiento circular uniforme , que es un movimiento en un círculo a una velocidad constante. En este movimiento, la fuerza centrípeta, la fuerza que apunta hacia el centro de un círculo, es siempre constante. Pero ese no es siempre el caso.

Si alguna vez ha movido una bolsa de compras en un círculo vertical, sabe que definitivamente no se siente igual en la parte superior e inferior de ese círculo. La bolsa de la compra se ralentiza en la parte superior del círculo y acelera en la parte inferior. La cantidad de fuerza que tienes que aplicar también cambia constantemente.

Esto sucede porque la gravedad apunta hacia abajo. En la parte superior del círculo, la gravedad apunta en la misma dirección que la tensión en la bolsa. En la parte inferior del círculo, la gravedad apunta en la dirección opuesta a la tensión. Y en el medio está … en el medio. Esto significa que la fuerza de tensión debe variar para compensar.

Entonces, ¿cómo analizamos el movimiento en un círculo vertical?

Ecuaciones

Ecuaciones energéticas para el movimiento

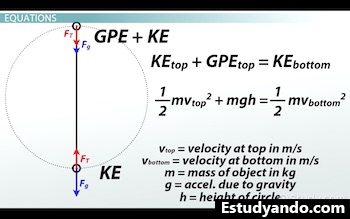Para analizar el movimiento en un círculo vertical y producir algunas ecuaciones, podemos usar una combinación de energía y fuerzas. La ecuación de energía para el movimiento es probablemente la más sencilla. En la parte superior, tenemos energía potencial gravitacional y energía cinética, y en la parte inferior, solo tenemos energía cinética. Entonces, la mitad mv al cuadrado en la parte superior más mgh en la parte superior es igual a la mitad mv al cuadrado en la parte inferior. Donde v-top es la velocidad en la parte superior en metros por segundo, v-bottom es la velocidad en la parte inferior, también en metros por segundo, m es la masa del objeto que se mueve en un círculo en kilogramos, g es la aceleración debida a la gravedad, que es 9,8 en la Tierra, y h es la altura del círculo, que se puede reemplazar con 2 veces el radio del círculo, 2r.

Ecuaciones de fuerza

Con respecto a las fuerzas, sabemos que la fuerza en un círculo es igual a la fuerza centrípeta, mv al cuadrado sobre r. Entonces, en la parte superior, tenemos la tensión y la gravedad contribuyendo a esta fuerza, lo que significa que la tensión en la parte superior (T-top, medida en newtons) más mg (la fuerza de gravedad) es igual a mv al cuadrado sobre r.

Pero en el fondo, la gravedad actúa para reducir la fuerza centrípeta. Entonces, aquí la fuerza de tensión menos mg será igual a mv al cuadrado sobre r. Entonces, ahora tenemos una ecuación para las fuerzas en la parte superior e inferior. Si sustituye una ecuación por otra, encontrará que la tensión en la parte inferior es igual a la tensión en la parte superior más 6 mg.

Ecuación de fuerza combinada

Podemos usar estas ecuaciones colectivamente para describir el movimiento en un círculo vertical y resolver problemas.

Problemas de práctica

Problema de práctica 1: Una pelota con una cuerda gira en un círculo vertical. Si la tensión en la cuerda en la parte superior del círculo es de 15 newtons y la bola pesa 0.1 kilogramos, ¿cuál es la tensión en la cuerda en la parte inferior del círculo?

En primer lugar, debemos escribir lo que sabemos. La tensión en la parte superior (T-top) es de 15 newtons y la masa de la pelota (m) es 0.1 kilogramos, y queremos encontrar la tensión en la parte inferior (T-bottom). Para resolver esto, podemos usar esta ecuación de tensión:

Diagrama y ecuación por ejemplo

Inserte los números y resuelva para T-bottom, y obtenemos 20.9 newtons. Y esa es nuestra respuesta.

Problema de práctica 2: Una bolsa de la compra se puede tratar de forma más sencilla. Si la bolsa de la compra pesa 1 kilogramo y la bolsa de la compra se gira en un círculo vertical con un radio de 0,1 metros y la bolsa de la compra se mueve a 2,5 m / s en la parte inferior del círculo, ¿qué tan rápido va en la parte superior del círculo? ?

Escribiendo lo que sabemos, vemos que la masa (m) es 1 kilogramo y el radio (r) es 0.1 metros. También sabemos que la velocidad en la parte inferior (v-bottom) es de 2.5 m / s. Se nos pide que encontremos la velocidad en la parte superior (v-top).

Aquí vamos a necesitar la ecuación energética. Sabemos todo en esta ecuación excepto v-top. Así que convierta v-top en el sujeto, introduzca números y resuelva, y obtenemos 1,53 m / s.

Resumen de la lección

El movimiento en un círculo vertical es bastante diferente al horizontal. Esto se debe a que la gravedad apunta hacia el centro del círculo en la parte superior y alejándose del centro del círculo en la parte inferior. Esto hace que la velocidad cambie (más lenta en la parte superior, más rápida en la parte inferior) y significa que la tensión también debe cambiar durante el movimiento.

Aquí hay algunas ecuaciones que derivamos para describir este movimiento:

Ecuaciones energéticas

La ecuación de energía dice que medio mv al cuadrado en la parte superior (la energía cinética) más mg2r en la parte superior (la energía potencial gravitacional) es igual a la mitad de mv al cuadrado en la parte inferior (la energía cinética en la parte inferior). Donde v-top es la velocidad en la parte superior medida en metros por segundo, v-bottom es la velocidad en la parte inferior, también medida en metros por segundo, m es la masa del objeto que se mueve en un círculo en kilogramos, g es la aceleración debida a la gravedad, que es de 9,8 en la Tierra, y r es el radio del círculo, medido en metros.

Ecuaciones de fuerza

También tenemos ecuaciones para describir las fuerzas en la parte superior e inferior, y una ecuación general que nos dice cómo la tensión en la parte superior se relaciona con la tensión en la parte inferior: que la tensión en la parte inferior es igual a la tensión en la parte superior más 6 mg. Podemos usar estas ecuaciones colectivamente para describir el movimiento en un círculo vertical y resolver problemas.

Los resultados del aprendizaje

Después de esta lección, tendrá la capacidad de:

• Explica por qué la velocidad y la tensión cambian durante el movimiento en un círculo vertical.
• Identificar las ecuaciones que describen el movimiento en un círculo vertical.