Modelo Black-Scholes: Fórmula y ejemplos

Un modelo matemático para los mercados financieros

Desde el comienzo del mercado de valores, los inversores han intentado obtener una ventaja. Los analistas de números han buscado durante mucho tiempo un modelo matemático que pudiera predecir el movimiento de los precios. Si de alguna manera pudieran descubrir la fórmula secreta, podrían volverse ricos más allá de sus sueños más locos.

El equipo de Fischer Black, Myron Scholes y Robert C Merton trató de hacer precisamente eso. Se les ocurrió un modelo matemático general para los mercados financieros que contienen instrumentos derivados. Al carecer de un nombre creativo, este modelo se conoció como el modelo Black-Scholes-Merton.

A partir de este modelo más grande, se hicieron modelos y ecuaciones más pequeños basados ​​en los mismos supuestos. Después de años de desarrollar el modelo, a Robert Merton se le atribuye haber mencionado por primera vez el ‘modelo de fijación de precios de opciones de Black-Scholes’ en 1973. Este modelo teórico podría ayudar a los creadores de mercado de opciones a valorar adecuadamente las opciones de todo tipo de instrumentos financieros. Su trabajo fue tan innovador que veinticuatro años después, en 1997, Robert C. Merton y Myron Scholes ganaron el Premio Nobel de Estudios Económicos por su trabajo.

Comprender las diversas entradas que se incluyen en el cálculo puede ayudar a los operadores a comprender si el mercado está sobrevalorando, subvalorando o fijando un precio justo en una opción. Aquí discutiremos los diversos factores en detalle y aprenderemos cómo usar el modelo para calcular los precios de las opciones.

La fórmula de Black-Scholes para el precio de las opciones

La fórmula de Black-Scholes es un modelo matemático para calcular el precio de las opciones de compra y venta. Dado que las opciones de compra y venta son claramente diferentes, hay dos fórmulas que dan cuenta de cada opción. Las opciones de compra le dan al tenedor de la opción el derecho a comprar las acciones subyacentes por un precio acordado en cualquier momento entre hoy y el vencimiento de la opción. Los operadores que creen que las acciones subyacentes subirán con el tiempo compran estas opciones de compra con la esperanza de ganar dinero.

Por otro lado, las opciones de venta le dan al tenedor de la opción el derecho a vender las acciones subyacentes por un precio acordado en cualquier momento entre hoy y el vencimiento de la opción. Los operadores que piensan que una acción va a bajar pueden comprar estas opciones de venta con la esperanza de ganar dinero si la acción baja.

La fórmula real de Black-Sholes parece complicada, pero en realidad es simple cuando se divide en lo básico. Los principales factores de la ecuación son:

• T = El tiempo hasta el vencimiento : cuánto tiempo hasta que expire la opción, en años;
• S = El precio actual : precio de la acción subyacente;
• K = El precio de ejercicio : el precio acordado de ejecución de la opción;
• r = La tasa libre de riesgo : una tasa que un inversionista podría obtener sin asumir ningún riesgo (típicamente el rendimiento de las letras del tesoro a 3 meses);
• σ = La volatilidad del precio : La volatilidad de los rendimientos de la acción subyacente, expresada como porcentaje.

Aquí está la notación matemática de la fórmula:

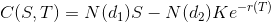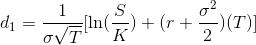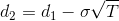Esta fórmula incluye la función N (x) que es la función de distribución normal estándar acumulativa. La función de distribución normal estándar acumulada se define como la probabilidad de que una variable aleatoria con distribución normal, una media de 0 y una varianza de ½ caiga en el rango de {-x, x}. Es un cálculo complicado que se ocupa del área bajo una curva de distribución normalizada.

Cálculo del valor teórico de la opción

Por el bien del cálculo de opciones, no es necesario que se convierta en un doctorado en matemáticas. Hay cientos de calculadoras en línea gratuitas que puede usar para ingresar valores fácilmente accesibles para calcular la fórmula de Black-Scholes.

Hagamos un cálculo de muestra con XYZ Corp Stock y definamos estos valores.

Tiempo hasta el vencimiento (T) = 1 año

Precio actual (S) = $ 120

Precio de ejercicio (K) = $ 100

Tasa libre de riesgo (r) = 1%

Volatilidad de precios (?) = 50%

Primero debe calcular los valores de d1 y d2, de modo que pueda incluir estos valores en la función de distribución normal estándar acumulativa.

Usando estos valores y una calculadora que encontré en línea, pude llegar a un valor teórico de $ 34.20 para la opción de compra. El precio de la opción de venta en el mismo ejercicio se deriva del cálculo de la opción de compra.

El uso de los mismos valores de entrada en la ecuación anterior nos da el precio teórico de la opción de venta en el mismo ejercicio. La calculadora en línea que usamos antes nos da un valor de $ 12.22 para la opción de venta.

¿Por qué alguien pasaría por todos estos problemas para hacer estos cálculos? Digamos que Sarah está buscando negociar con opciones sobre acciones de XYZ Corp, pero no está segura de qué opción quiere comprar. Cada fecha de vencimiento de la opción tiene varias opciones para elegir. Suponiendo que ella piensa que las acciones de XYZ Corp van a subir durante el próximo año y quiere comprar una opción de compra, tiene muchos precios de ejercicio diferentes para considerar.

Al conocer el valor teórico de varias opciones diferentes en varios strikes, puede compararlas con el precio de negociación actual de las opciones para encontrar oportunidades. Mirando el ejercicio de $ 100 en el ejemplo con un valor teórico de $ 34.20, Sarah puede comparar el precio de negociación actual de la opción. Si la opción se cotiza por debajo de $ 34,20, entonces la opción puede estar infravalorada por el mercado. Al invertir en opciones de bajo precio como esta, Sarah se ha dado un poco de ventaja. Si puede descubrir grandes desviaciones del valor teórico en la cadena de opciones, puede darse una ventaja aún mayor en el mercado.

No se entusiasme demasiado tratando de descubrir desviaciones gigantes de los precios de mercado y los precios de opciones teóricas. Los creadores de mercado conocen bien el método Black-Scholes y tienden a fijar el precio de las opciones en consecuencia.

Resumen de la lección

La fórmula de Black-Scholes es un modelo matemático para calcular el precio de las opciones de compra y venta. La fórmula tiene en cuenta:

El tiempo hasta el vencimiento : cuánto tiempo hasta el vencimiento de la opción, en años;

El precio actual : el precio actual de la acción subyacente;

El precio de ejercicio : El precio acordado de ejecución de la opción;

La tasa libre de riesgo : la tasa que un inversionista podría obtener sin asumir ningún riesgo (típicamente el rendimiento de las letras del tesoro a 3 meses);

La volatilidad del precio : La volatilidad de los rendimientos de la acción subyacente, expresada como porcentaje.

Al calcular estos valores teóricos, los operadores de opciones toman decisiones basadas en la probabilidad sobre qué opciones comprar y vender.