Prisma hexagonal: propiedades, fórmula y ejemplos
Prisma hexagonal
Un hexágono es un polígono de 6 lados. Un prisma es un objeto tridimensional que tiene dos extremos paralelos, llamados bases, que tienen el mismo tamaño y forma. Los lados de un prisma, llamados caras , son paralelogramos. Según estas definiciones, probablemente le resulte fácil darse cuenta de que un prisma hexagonal es un prisma con dos bases que son hexágonos y seis caras que son rectángulos.
 |
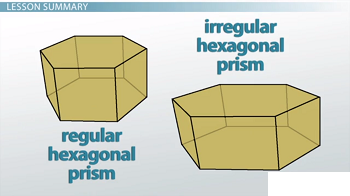
Los prismas hexagonales pueden ser regulares o irregulares. Un prisma hexagonal regular es un prisma hexagonal con hexágonos regulares como base. Si estás imaginando un hexágono en este momento, probablemente estés imaginando un hexágono donde todos los lados tienen la misma longitud. Así es básicamente como se ven las bases del prisma.
Un prisma hexagonal irregular es lo contrario. Tiene bases hexagonales que son irregulares, por lo que los lados de sus bases hexagonales no tienen todos la misma longitud.
Hay prismas hexagonales que se pueden observar en el mundo que nos rodea. Algunos ejemplos incluyen un lápiz (antes de afilarlo, por supuesto), una nuez o una piedra, entre muchos otros.
Debido a que los prismas hexagonales aparecen en todas partes, puede ser útil para algunos de nosotros saber cómo calcular el área de superficie y el volumen de estos objetos.
Área de superficie de un prisma hexagonal
El área de superficie de un objeto 3D es el área de todas las superficies del objeto sumadas. Por lo tanto, el área de la superficie de un prisma hexagonal sería el área de sus dos bases más el área de sus seis caras. Es decir, Área de superficie ( SA ) = 2 * (área de la base del hexágono) + área de la cara 1 + área de la cara 2 + área de la cara 3 + área de la cara 4 + área de la cara 5 + área de la cara 6. Esto es también la fórmula que usaríamos si nuestro prisma hexagonal fuera irregular. Bastante sencillo, ¿verdad?
Cuando se trata de un prisma hexagonal regular, podemos simplificar esta fórmula. Pero antes de hacer esto, necesitamos conocer algunos hechos. Primero, observe que en un prisma hexagonal regular, todas las caras rectangulares tienen la misma área. Para encontrar el área de uno de estos rectángulos, podemos multiplicar su largo por su ancho. Su longitud es la altura del prisma (llamado h ) y el ancho es la longitud de uno de los lados de las bases hexagonales (llamémoslo s ). Por lo tanto, el área de una de las caras del rectángulo es sh, y las seis caras tienen la misma área.
En segundo lugar, notamos que un hexágono regular tiene una apotema. Una apotema es la línea desde el centro del hexágono hasta el centro de uno de los lados del hexágono.
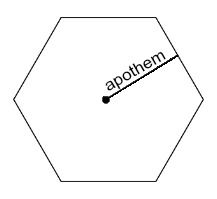 |
Cuando conocemos la longitud de la apotema de un hexágono regular, a , y la longitud de uno de sus lados, s, podemos encontrar el área del hexágono usando la fórmula A = 3 como.
 |
Usando estos hechos, podemos simplificar nuestra fórmula de área de superficie.
 |
Esta simplificación da que el área de la superficie de un prisma hexagonal regular es SA = 6 s ( a + h ), donde s = longitud del lado de la base, a = longitud del apotema y h = altura del prisma.
Por ejemplo, supongamos que quisiéramos saber el área de superficie de un edificio que tiene la forma de un prisma hexagonal regular que tiene una longitud de lado de base de 40 pies, una longitud de apotema de 35 pies y una altura de 20 pies. Para hacer esto, introduciríamos s = 40, a = 35 y h = 20 en nuestra fórmula para obtener SA = 6 * 40 * (35 + 20) = 240 (55) = 13,200 pies cuadrados.
Volumen de un prisma hexagonal
En caso de que necesite un resumen rápido, el volumen de un objeto tridimensional es la cantidad de espacio dentro del objeto. Cuando queremos encontrar el volumen de un prisma, multiplicamos el área de su base por su altura. En el caso de un prisma hexagonal, nuestro volumen sería V = (Área de la base del hexágono) (altura del prisma). Como encontrar el área de la superficie, esa también es la fórmula que usamos para un prisma hexagonal irregular.
¿Recuerda cómo, después de simplificar la ecuación original, encontramos que el área de la base hexagonal del prisma está dada por 3 como , donde a = longitud del apotema y s = longitud del lado? Por lo tanto, si dejamos que h sea la altura del prisma, entonces el volumen de un prisma hexagonal regular se puede encontrar usando la fórmula V = (3 as ) ( h ) = 3 cenizas.
Por ejemplo, supongamos que queremos saber el volumen de un lápiz sin punta y sin borrador. Las bases hexagonales del lápiz tienen una longitud lateral de 0,14 pulgadas y una longitud de apotema de 0,125 pulgadas. La altura del lápiz es de 4 pulgadas. Para encontrar el volumen del lápiz, introducimos s = 0.14 pulgadas, a = 0.125 pulgadas y h = 4 pulgadas en nuestra fórmula de volumen para obtener V = 3 * 0.125 * 0.14 * 4 = 0.21 pulgadas cúbicas. El volumen de nuestro lápiz es de 0,21 pulgadas cúbicas.
Resumen de la lección
Un prisma hexagonal es un objeto tridimensional que tiene dos hexágonos como bases paralelas entre sí y seis caras rectangulares. Hay prismas hexagonales regulares e irregulares . Las bases hexagonales de los prismas hexagonales regulares tienen lados que son todos iguales en longitud. Este no es el caso de un prisma hexagonal irregular, que tiene lados que tienen diferentes longitudes. Para encontrar el área de la superficie de un prisma hexagonal irregular, simplemente sumamos las áreas de las bases y caras del prisma.
Para encontrar el área de la superficie de un prisma hexagonal regular, podemos usar la fórmula SA = 6 s ( a + h ), donde s = longitud del lado de la base, a = longitud del apotema y h = altura del prisma. Para encontrar el volumen de un prisma hexagonal regular, podemos usar la fórmula V = 3 ceniza, donde a = longitud de la apotema, s = longitud de un lado de la base y h = altura del prisma. Estas definiciones y fórmulas nos permiten comprender mejor los prismas hexagonales y cómo trabajar con ellos.
Notas de prisma hexagonal
 |
| Descripción | Ecuaciones |
|---|---|
| Un prisma hexagonal tiene: * Dos bases hexagonales que son paralelas entre sí * Seis caras rectangulares * Una apotema |
* Superficie: SA = 6 s ( a + h ) * Volumen: V = 3 cenizas |
Los resultados del aprendizaje
A través del proceso de exploración de esta lección sobre prismas hexagonales, desarrollará su capacidad para:
- Ilustra un prisma hexagonal
- Reconocer la diferencia entre prismas hexagonales regulares e irregulares
- Calcular el área de superficie y el volumen de un prisma hexagonal
Articulos relacionados
- ¿Cuáles son las Propiedades de la Materia?
- Errores comunes al Invertir en Propiedades
- ¿Qué es el Salario Real? Fórmula y ejemplos
- Propiedades de una sustancia: Definición, tipos y ejemplos
- Propiedades de Carnes, Pescados, Aves y Alternativas a la Carne
- Conservación de Alimentos: Propiedades y Tipos
- Principio de Arquímedes: historia, fórmula y ejemplos
