Graficar funciones polinomiales factorizables

Graficar polinomios factorizables

Cuando se grafica un polinomio en una cuadrícula de coordenadas, se crea una curva continua para todos los valores de x desde el infinito negativo hasta el infinito positivo. Una de las principales preocupaciones al graficar un polinomio es encontrar dónde la gráfica se cruza con el eje x. Esta tarea es más fácil si el polinomio es un polinomio factorizable. Esta lección definirá los términos polinomio y factorizable. También podrá encontrar los ceros de funciones polinomiales factorizables y determinar su comportamiento final.

Polinomios

Los polinomios son funciones que constan de uno o más términos monomiales que se han conectado mediante suma o resta. Cada término tiene una parte numérica y una parte variable. La variable se puede elevar a cualquier potencia que sea un número natural.

1. f (x) = 3x 3 + 2x 2 – 7x + 8
2. g (x) = 10 x 2 – 90
3. h (x) = 8

Polinomios factorizables

Un polinomio factorizable es una función que se puede dividir en dos o más factores. Estos factores serán de un grado menor que la función original y cuando se multipliquen le darán la función original. Ejemplos de polinomios factorizables:

1. f (x) = x 2 – 4x – 12 factores como (x – 6) (x + 2)
2. g (x) = x 2 – 25 factores como (x – 5) (x + 5)
3. h (x) = x 3 – 7x 2 – 8x – 12 factores como (x + 2) (x + 2) (x – 3)

Graficar polinomios factorizables

Para graficar un polinomio factorizable, necesita saber dos cosas, dónde se encuentran los ceros y el comportamiento final.

Ceros

Los ceros de una función polinomial son los valores de x que hacen que el valor de y sea igual a cero. En el gráfico, los ceros son los puntos en los que el gráfico de la función cruza el eje x. Puedes encontrar el valor de estos ceros estableciendo el polinomio igual a cero y resolviendo para x. Si se puede factorizar un polinomio, entonces debe establecer esos factores en cero.

x 2 – 7x + 10 = 0 en forma factorizada es (x – 5) (x – 2) = 0.

Cuando un polinomio está en forma factorizada, puedes aplicar la regla del producto cero para encontrar los ceros de esta función. La regla del producto cero establece que si dos o más artículos se multiplican y el producto es cero, al menos uno de los artículos tenía que ser igual a 0.

Entonces, cuando (x – 5) (x – 2) = 0 ya sea x – 5 = 0 o x – 2 = 0. Resolver para x da 2 y 5 para los ceros de la función f (x) = x 2 – 7x + 10. Este es el primer paso para graficar un polinomio factorizable.

Comportamiento final

Para graficar un polinomio factorizable, necesitará saber cómo se comporta la función cuando x es un número positivo muy grande y un número negativo muy grande. Cuando x es un número positivo o negativo grande, y también será un número positivo o negativo muy grande. Entonces, en sus extremos, un polinomio irá al infinito positivo o negativo.

El término principal del polinomio indicará qué tipo de comportamiento final exhibe el polinomio. El término principal de un polinomio es el término que tiene el mayor exponente.

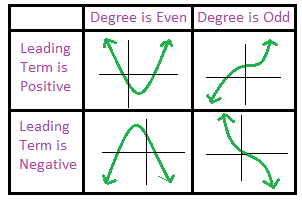
• Todos los polinomios que tienen un coeficiente principal con un grado que es un número par tendrán un comportamiento final que es el mismo en cada extremo. Ambos irán al infinito positivo o ambos irán al infinito negativo. Un coeficiente principal negativo significa que ambos van al infinito negativo. Un coeficiente positivo significa que ambos van al infinito positivo.
• Si el grado es un número impar, el comportamiento final se dividirá. Uno va al infinito negativo y el otro al infinito positivo. Un coeficiente negativo significa que cuando x es un número positivo muy grande, y es un número negativo grande. Un coeficiente positivo significa que cuando x es un número positivo muy grande, y también es un número positivo grande.

Comportamiento final de los polinomios

Poniendolo todo junto

Grafica el polinomio f (x) = 2x 3 – 4x 2 – 10x + 12

1. ¿Se puede factorizar? Sí f (x) = 2 (x – 1) (x + 2) (x – 3)
2. Hallar los ceros 0 = 2 (x – 1) (x + 2) (x – 3) Ceros en 1, -2, 3
3. Trace los ceros en una cuadrícula xy.
4. Determine el comportamiento final. El término principal es 2x 3 . El grado es un número impar y el coeficiente es positivo. Eso significa que los polinomios van al infinito negativo cuando x es muy negativo y al infinito positivo cuando x es un número positivo grande.
5. Grafique el comportamiento final en la cuadrícula xy.
6. Para obtener un punto adicional, grafica la intersección con el eje y (establece x igual a cero). (0, 12)
7. Conecte todos sus puntos y comportamiento final con una curva suave.
   

   Graficar un polinomio factorizable

Resumen de la lección

Si una función polinomial es factorizable, puedes graficar la función encontrando los ceros y determinando el comportamiento final. Para encontrar los ceros de una función polinomial, factorícela y establezca cada uno de los factores igual a cero.

El comportamiento final de un polinomio se basa en el término principal. Incluso los exponentes numéricos tienen el mismo comportamiento final en cada extremo. Los exponentes de números impares en el término principal tendrán un comportamiento de extremo dividido, un extremo que va al infinito positivo y el otro al infinito negativo. El signo del coeficiente principal indica si los extremos de la función van al infinito positivo o negativo para un exponente de número par o qué extremo va al infinito positivo y qué extremo va al infinito negativo con un exponente de número impar. Poner toda esta información en una cuadrícula xy te da la gráfica de un polinomio factorizable.