
Clave de respuestas para asignaciones de educación en el hogar de precálculo
Calificación y rúbrica
Cada una de las preguntas para las siguientes asignaciones vale 2 puntos; 1 punto por mostrar el trabajo y 1 punto por la respuesta correcta. Puede calificar usando una rúbrica como esta:
| Pregunta | Pasos mostrados (1 pt) | Respuesta correcta (1 punto) |
|---|---|---|
| Pregunta 1 | ||
| Pregunta 2 | ||
| Pregunta 3 | ||
| Pregunta 4 | ||
| Pregunta 5 | ||
| Pregunta 6 | ||
| Pregunta 7 | ||
| Pregunta 8 | ||
| Pregunta 9 | ||
| Pregunta 10 | ||
| Total de la columna | ||
| Total de la asignación: |
Considere imprimir o guardar la rúbrica para mantener un registro de las calificaciones de las tareas.
Funciones exponenciales y clave de respuestas para la asignación de funciones logarítmicas
1. Expande la expresión logarítmica: log (x 2 y 5 )
Utilice la propiedad del producto y la propiedad de potencia:
2 log (x) + 5 log (y)
Ver propiedades logarítmicas
2. Condensar la expresión logarítmica: 2log (x) – 3log (y) + log (5)
Utilice la propiedad del producto, la propiedad del cociente y la propiedad de la potencia:
log (5x 2 / y 3 )
Ver propiedades logarítmicas
3. Resuelve para x: log 4 (22) = x
Utilice la fórmula de cambio de base:
log (22) / log (4) = 2,23
Ver cómo evaluar logaritmos
4. Resuelve para x: 16 (x + 1) = 4 (3x)
Primero, iguale las bases:
4 2 (x + 1) = 4 (3x)
4 (2x + 2) = 4 (3x)
2x + 2 = 3x
x = 2
Ver cómo resolver ecuaciones exponenciales
5. La población de Small Town USA es de 5,000 y se espera un crecimiento del 3% en 10 años. ¿Cuál es la población total después de 10 años?
Usa la fórmula y = ab x donde y es el valor final, a es el valor inicial, b es el número repetidamente multiplicado en cada paso y x es el número de veces que multiplicamos.
Aquí, y es lo que estamos tratando de encontrar, a es 5,000, b es 3%, que escribimos como 1.03, y x es 10.
y = (5000) (1,03) 10
y = 6.720
Ver qué es una función exponencial
6. Si desea ahorrar $ 12,000 en siete años y cree que puede invertir al 7% de interés, ¿cuánto es su depósito inicial?
Usa la fórmula y = ab x donde y es el valor final, a es el valor inicial, b es el número repetidamente multiplicado en cada paso y x es el número de veces que multiplicamos.
Aquí, a es lo que estamos tratando de encontrar, y es 12,000, b es 7%, que escribimos como 1.07, yx es 7.
12.000 = (a) (1,07) 7
12.000 = 1,6a
a = 7500
Ver qué es una función exponencial
7. Dibuje las siguientes funciones exponenciales (Nota: no es necesario trazarlas con precisión):
a. f (x) = 2 x + 2
segundo. f (x) = 2 -x – 1
C. f (x) = 2 x – 3
a.
 |
segundo.
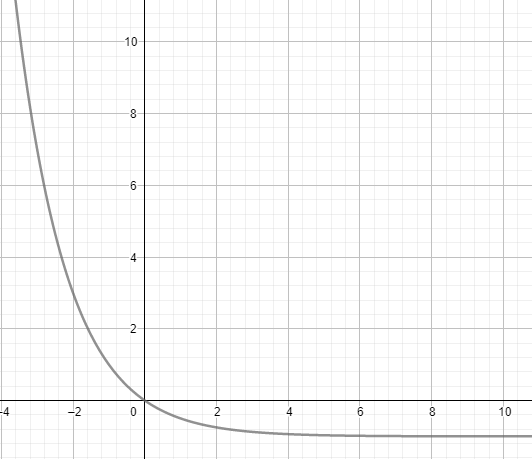 |
C.
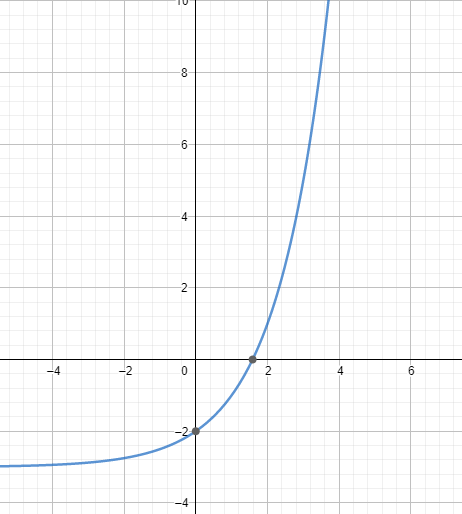 |
8. Encuentre la función inversa de: f (x) = log 4 – 2
2 (4 + 2x) – 1
9. Dibuje las siguientes funciones logarítmicas:
a. f (x) = log 2
segundo. f (x) = log 2 – 1
a.
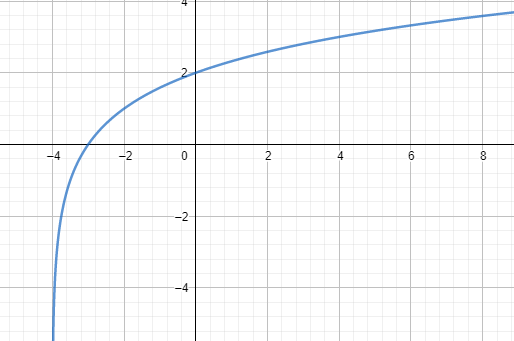 |
segundo.
 |
10. Use la fórmula de cambio de base para evaluar a dos lugares decimales: log 7 (100)
log 7 (100) = log (100) / log (7) = 2.37
Clave de respuestas de asignación de trabajo con desigualdades
1.Resolver y graficar 2x + 6 ≥ 28
2x + 6 ≥ 28
2x ≥ 22
x ≥ 11
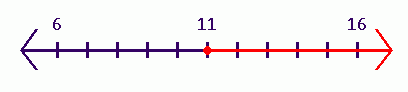 |
Ver cómo graficar dos desigualdades variables
2. Resuelve y grafica 8> 4 – x ≥ -1
8> 4 – x ≥ -1
4> – x ≥ -5
-4 <x ≤ 5
 |
Ver cómo graficar dos desigualdades variables
3. Grafica y <2x + 3
La intersección con el eje y es 3
La intersección con el eje x es -1,5
La línea está punteada porque es menor, no menor o igual que
El área sombreada está debajo del gráfico porque es menor que
 |
Ver cómo graficar dos desigualdades variables
4. Resuelve y representa gráficamente el sistema de desigualdades, etiquetando cada ecuación en la gráfica: 2y – 3 ≤ 4x + 1; 4y + 8> -8; x <1
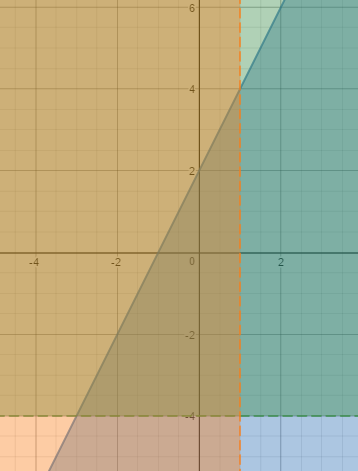 |
Ver sistemas de desigualdades
5. Resuelve y representa gráficamente y <| x – 3 | + 2
 |
Consulte Cómo resolver una desigualdad de valor absoluto y utilice la notación de conjuntos
6. Como segunda parte de esta tarea, cree su propia desigualdad utilizando un escenario del mundo real de su vida. Por ejemplo, ‘Mi objetivo es ganar al menos $ 100 vendiendo galletas Girl Scout a $ 4 la caja. Hasta ahora, he vendido 10 cajas ‘. La desigualdad para esta situación sería: 40 + 4x ≥ 100.
7. Resuelve la siguiente desigualdad cuadrática: -2x 2 + 4x + 6 <0
x> 3, x <-1
Consulte la lección sobre cómo resolver desigualdades cuadráticas utilizando dos binomios.
8. Resuelve la siguiente desigualdad cuadrática: x 2 + 3x + 2 <-x 2 + 2
-3/2 <x <0
Consulte la lección sobre cómo resolver desigualdades cuadráticas utilizando dos binomios.
9. Grafique este sistema de desigualdades y luego resalte y etiquete la solución para el sistema de desigualdades en el mismo conjunto de ejes:
y> x 2
y <2x 2 + 2
y <- x 2 + 4x + 3
La solución al sistema de desigualdades es el área donde todas las áreas sombreadas se superponen.
 |
10. Resuelve la siguiente desigualdad racional:
 |
Solución:
x> -2/3
x ≤ -5
Clave de respuestas para la asignación de aplicaciones trigonométricas
1. Identifique el período, la amplitud y el desplazamiento de fase de y = -3sin (4x – π)
Periodo: π / 2
Amplitud: 3
Cambio de fase: π / 4
Ver Graficar transformaciones de seno y coseno
2. Cada lado de un triángulo equilátero mide 9 cm. Encuentra el área.
 |
Si dibujas una bisectriz de ángulo, obtienes dos triángulos 30-60-90. La hipotenusa es 9. El cateto corto es 4.5. La pierna larga es 4.5√3.
A = 1/2 * b * h
A = 1/2 * 9 * 4,5√3,5
A = 35,07 cm 2
3. En el triángulo PQR, el lado PQ es 85, el lado QR es 72 y el ángulo R es 47 grados. Usa la ley de los senos para encontrar el ángulo Q.
 |
85 / (¿pecado? (47)) = 72 / (¿pecado? (P))
85 / .73 = 72 / (¿pecado? (P))
116 = 72 / (¿pecado? (P))
116 * sin (P) = 72
pecado (P) = .62
pecado-1 (.62) = 38
Ángulo P = 38
Ángulo Q = 180 – 38 – 47 = 95
Ver Ley de los senos: definición y aplicación
4. Exprese cos (2x) en términos de sen x y luego nuevamente en términos de cos x.
cos (2x) = cos 2 x – sin 2 x
cos (2x) = (1 – sin 2 – sin 2 x
cos (2x) = 1 – 2 sen 2 x
cos (2x) = cos 2 x – sin 2 x
cos (2x) = cos 2 x – (1 – cos 2 x)
cos (2x) = 2cos 2 x – 1
Ver la fórmula del doble ángulo
5.Resuelva para cotΘ: π (sinΘcosΘ) + sin 2 Θ = 1
Sustituye sen 2 Θ + cos 2 Θ por 1:
π (sinΘcosΘ) + sin 2 Θ = sin 2 Θ + cos 2 Θ
Resta sin 2 Θ de ambos lados:
π (sinΘcosΘ) = cos 2 Θ
Dividir ambos lados por sinΘcosΘ:
π = cos 2 Θ / (sinΘcosΘ)
Cancelar un cosΘ del numerador y denominador:
π = cosΘ / sinΘ
π = cunaΘ
Consulte la lista de identidades de activación básicas
6. Usa la ley de los cosenos para hallar la longitud de AB.
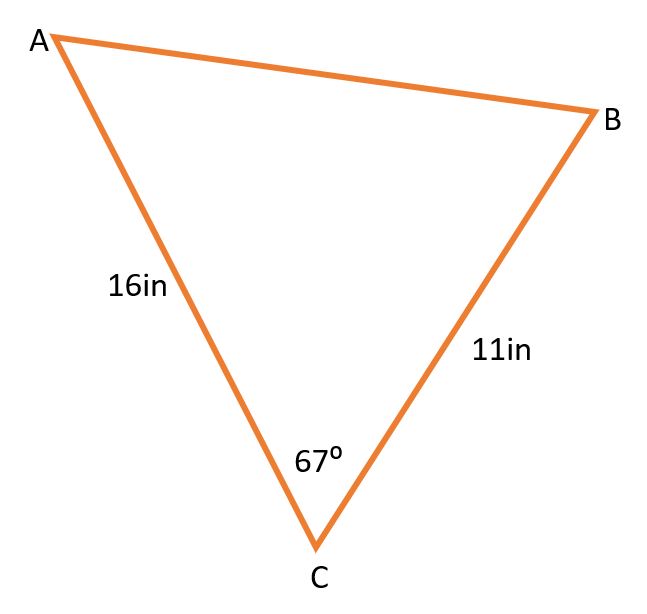 |
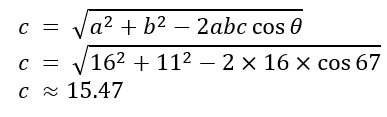 |
7. Evalúe sin (3π / 2) sin (π / 4) – cos (3π / 2) cos (π / 4)
Necesitamos usar nuestra identidad de diferencia de coseno.
cos (a + b) = cos (a) cos (b) – sin (a) sin (b)
Observe que el término cos y el término pecado tienen el signo opuesto.
Si multiplicamos ambos lados de la identidad de diferencia de coseno por -1, obtenemos:
-cos (a + b) = sin (a) sin (b) – cos (a) cos (b)
Por lo tanto, sin (3π / 2) sin (π / 4) – cos (3π / 2) cos (π / 4) = -cos (3π / 2 + π / 4) = – 1 / √2 = -0,71
